Centre for Geotechnical Science and Engineering
Risk Assessment in Geotechnical Engineering
Key Researchers: Jinsong Huang, Richard Kelly, Andrei Lyamin
INTRODUCTION
It is estimated that 20% to 50% of construction projects have time and/or cost over-runs and an important contributing factor is unforseen or variable ground conditions. Uncertainty can be reduced through extensive site investigation, but the amount of work required to considerably reduce uncertainty can be uneconomic. Uncertainty can be managed through conservative design or by providing a large contingency to a project, both of which drive up costs. It is possible that many apparently successful geotechnical projects may have cost significantly more than necessary. Thus there is a compelling need for geotechnical engineers to better quantify uncertainty and its consequences in order to improve project outcomes, particularly for large infrastructure projects.
QUANTITAITVE RISK ASSESSMENT
By the very nature of their origins, geotechnical materials such as soils and rocks feature variable engineering properties. This variability is rarely taken into account directly in traditional geotechnical analysis. Instead, some “representative average” or “appropriately conservative” property is usually assumed across the whole region of interest. The evaluation of the safety of geotechnical projects is calculated using analytical or numerical methods and quantified via a safety factor, to keep the probability of failure to acceptable levels. The factor of safety itself can be overly conservative in some cases. It is common to use the same safety factor for different types of applications, without regard to the degree of uncertainty involved in its calculation. Through regulation or tradition, the same safety factor is often applied to conditions that involve widely varying degrees of uncertainty. This approach does not account for the consequences of variability or failure. High probability events attracting a high factor of safety may have negligible consequences, and could be designed more economically. The deterministic approach also does not necessarily reflect the risk appetite of the client or contracto,r and does not allow them to make informed decisions. In the past few years, a number of probabilistic methods, where risk is explicitly quantified, have been developed in the PRCGSE. In particular, Huang et al. (2013) developed a quantitative risk assessment framework, where failures and consequences are assessed explicitly through Monte Carlo simulations. Figure 1 shows a three dimensional slope where both failure and consequence are simulated numerically.
Figure 1: a) Quantitative risk assessment of slope instability where spacial variability is modelled direclty and consequence is explicitly quantified.
In addition, a number of probabilistic approaches have been proposed to assess the influence of spatial variability on the stability of geotechnical structures. Amongst such methods, the Random Finite Element Method (RFEM) is very promising and has been used extensively in recent times. RFEM combines random field theory with the non-linear finite element method (FEM). Recently, researchers in the CGSE have combined the finite element limit analysis (FELA) method with random field theory to predict the collapse state of geotechnical structures in a direct and cost-effective manner. Figure 2 shows a two-layer slope where failure and consequence are assessed through adaptive remeshing.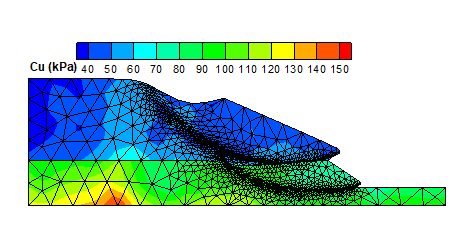
Figure 2: Failure mechanicsms observed via adaptive mesh analysis
BAYESIAN STATISTICAL METHODS
Currently, geotechnical engineers use allowable stress design (WSD/ASD); Load and Resistance Factor Design (LRFD, United States); Limit State Design (LSD, Canada); and Partial Factors Design (PFD, Europe, Australia) to design structures which have an acceptable probability of failure. The emphasis is primarily on the re-distribution of the original global factor of safety into separate load and resistance factors (or partial factors), where risk is not explicitly quantified. These types of semi-probabilistic design codes lead to a dilemma where geotechnical engineers produce deterministic designs on the assumption that risk is controlled, but then find themselves spending the construction period trying to manage variability and risk. Geotechnical risk management during construction is often done using the observational method along with experience and engineering judgement. The Bayes theorem provides a theoretical framework for updating predictions based on monitoring data. This can be done in real-time, allowing engineers to benefit from constantly updated predictions. In this way, the probability of an event occurring can be quantified continuously.
Figure 3: Consolidation settelent prediction
Bayesian methods have been successfully applied to the prediction of long-term settlement of the embankment at the National Soft Soil Test Facility. Figure 3 shows a comparison between settlements calculated using the posterior distributions and the measurements. The fit between the measurements and the posterior calculation is excellent after about 116 days of measurements. Offshore applications can benefit from this approach too. Probabilistic predictions of peak stress, and the depth at which the punch-through will occur, during the installation of a spudcan foundation can be continuously updated by incorporating monitoring data (Cassidy et. al 2015). The prior probability of punch-through is first calculated as shown in Fig. 4a. These contours represent the probability of occurrence of punch-through. If a set of monitoring data has been acquired at consecutively deeper penetrations, the posterior probability of punch-through informs the engineer that a punch-through is becoming less likely to occur, thereby providing a measure of confidence during the installation.
Figure 4: Prior and posterior probability of punch-trhough after the aqucisition of three sets of monitoring data.
CONCLUSIONS
As clients increasingly demand more rational risk control, risk management will become an essential part of the design, analysis, construction and management of engineering projects. It is anticipated that such risk management will be incorporated into many aspects of geotechnical engineering projects on a daily basis. Barriers to achieving this goal are the development of reliable, efficient and widely available risk analysis and management tools, and training geotechnical engineers to think stochastically. It is thus necessary to train Australian students and postgraduate researchers in an emerging technological field that involves statistics and probability theory, numerical simulation and reliability analysis.
REFERENCES
Ali A, Lyamin AV, Huang J, Sloan SW and Cassidy MJ. (2017), Undrained stability of a single circular tunnel in spatially variable soil subjected to surcharge loading.Computers and Geotechnics, 84: 16-27
Cassidy M, Li J, Hu P, Uzielli M, Lacasse S (2015), Deterministic and probabilistic advances in the analysis of Spudcan behaviour ISFOG 2015
Huang J, Lyamin AV, Griffiths DV, Krabbenhoft K, Sloan SW. (2013), Quantitative risk assessment of landslide by limit analysis and random fields, Computers and Geotechnics, 53:60-67
Dong Z, Huang J, Kelly R, Li D, Sloan SW (2018), Embankment prediction using testing data and field monitored behaviour: A Bayesian updating approach Computers and Geotechnics, 93:150–162
The University of Newcastle acknowledges the traditional custodians of the lands within our footprint areas: Awabakal, Darkinjung, Biripai, Worimi, Wonnarua, and Eora Nations. We also pay respect to the wisdom of our Elders past and present.
