Dr Stephan Tornier
ARC DECRA
School of Information and Physical Sciences
- Email:stephan.tornier@newcastle.edu.au
- Phone:0240550960
Career Summary
Biography
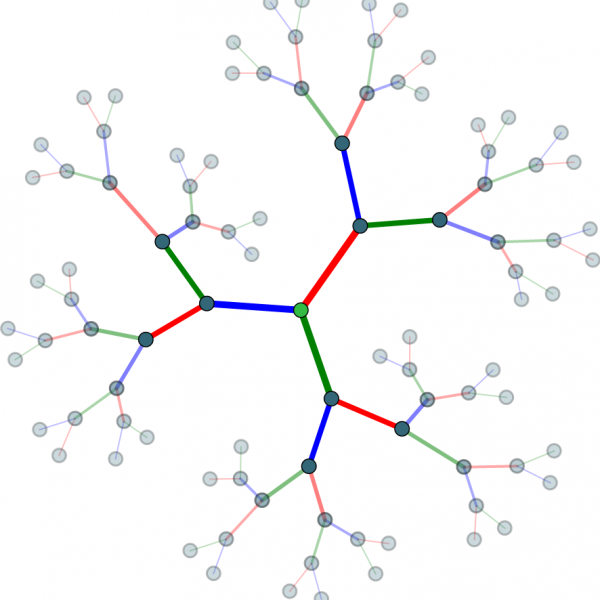
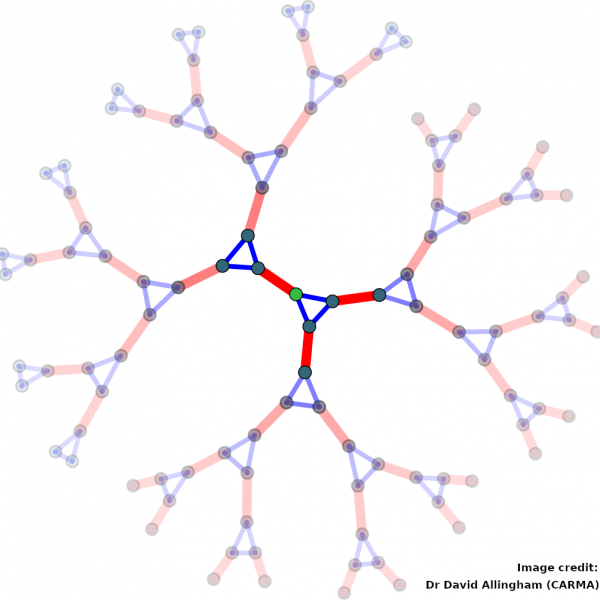
I am an early to mid-career academic in the area of group theory, the mathematical formalisation of the intuitive concept of symmetry. Specifically, I am concerned with the symmetry of infinite discrete structures, such as graphs or networks, which are prevalent in our digital world and therefore constitute an important field of applications of mathematics to technology. My research combines the latest theoretical insights into such structures with computational approaches in order to advance our understanding of the underlying mathematical objects.
Throughout, my research journey has been driven by a strong commitment to collaboration. I have had the privilege to collaborate with distinguished researchers, both within and beyond my institution, to expand the scope of inquiry and pave the way for innovative breakthroughs, such as software with the potential to accelerate research across the field.
Teaching
Beyond my research, I am deeply dedicated to sharing the beauty of mathematics with others. As an experienced lecturer and supervisor, I strive to guide and inspire students at various levels and thereby educate the next generation of researchers. My efforts have ranged from creating videos for high-school students, via first-year projects in Puzzles, Codes and Groups and AMSI summer scholar projects to the supervision of Honours, Master's and Ph.D. students.
Background
My academic journey began with a solid foundation in mathematics, physics, and geography during high school in Northern Germany. With a particular interest in astronomy and theoretical physics at the time, I decided to pursue a Bachelor's degree in mathematics at ETH Zurich, including an enriching exchange program at the Australian National University in Canberra.
Building on this foundation, I continued my studies in mathematics with a Master's and Ph.D. at ETH Zurich. This allowed me to delve deeply into the fascinating world of group theory, specifically locally compact groups. Whereas my studies focused on the connected case of Lie groups, my Master's thesis concerned rigidity phenomena associated to Property (T) and amenability in general locally compact groups. Finally, in my Ph.D. thesis, I transitioned to the opposite side of the spectrum by studying totally disconnected locally compact groups, such as groups acting on trees.
Qualifications
- Doctor of Science, Swiss Federal Institute of Technology - Zurich
- Bachelor of Science (Mathematics), Swiss Federal Institute of Technology - Zurich
- Master of Science (Mathematics), Swiss Federal Institute of Technology - Zurich
Keywords
- Algebra
- Group theory
- Topological and computational group theory
- Totally disconnected, locally compact groups
Languages
- German (Mother)
- English (Fluent)
Fields of Research
| Code | Description | Percentage |
|---|---|---|
| 490405 | Group theory and generalisations | 100 |
Professional Experience
UON Appointment
| Title | Organisation / Department |
|---|---|
| Lecturer | University of Newcastle School of Information and Physical Sciences Australia |
Academic appointment
| Dates | Title | Organisation / Department |
|---|---|---|
| 1/1/2017 - 31/8/2017 | SNSF Fellow | University of Newcastle School of Mathematical and Physical Sciences Australia |
| 1/6/2016 - 31/12/2016 | Research Assistant | University of Newcastle School of Mathematical and Physical Sciences Australia |
| 1/5/2013 - 31/8/2016 | Teaching Assistant | ETH Zurich Department of Mathematics Switzerland |
Publications
For publications that are currently unpublished or in-press, details are shown in italics.
Chapter (2 outputs)
| Year | Citation | Altmetrics | Link | |||||
|---|---|---|---|---|---|---|---|---|
| 2025 |
Tornier S, Ferov M, Willis G, 'Computational Aspects of Totally Disconnected Locally Compact Groups' (2025)
|
|||||||
| 2018 |
Garrido A, Glasner Y, Tornier S, 'Automorphism groups of trees: generalities and prescribed local actions', 447, 92-116 (2018) [B1]
|
Open Research Newcastle | ||||||
Journal article (5 outputs)
| Year | Citation | Altmetrics | Link | |||||
|---|---|---|---|---|---|---|---|---|
| 2023 |
Tornier S, 'GROUPS ACTING on TREES with PRESCRIBED LOCAL ACTION', Journal of the Australian Mathematical Society, 115, 240-288 (2023) [C1]
|
Open Research Newcastle | ||||||
| 2020 |
Carter M, Tornier S, Willis G, 'On free products of graphs', Australasian Journal of Combinatorics, 78, 154-176 (2020) [C1]
|
Open Research Newcastle | ||||||
| 2019 |
Bywaters T, Tornier S, 'Willis theory via graphs', Groups, Geometry, and Dynamics, 13, 1335-1372 (2019) [C1]
|
Open Research Newcastle | ||||||
| 2018 |
Tornier S, 'Prime localizations of Burger-Mozes-type groups', Journal of Group Theory, 21, 229-240 (2018) [C1]
This article concerns Burger-Mozes universal groups acting on regular trees locally like a given permutation group of finite degree. We also consider locally isomorphic... [more] This article concerns Burger-Mozes universal groups acting on regular trees locally like a given permutation group of finite degree. We also consider locally isomorphic generalizations of the former due to Le Boudec and Lederle. For a large class of such permutation groups and primes p we determine their local p-Sylow subgroups as well as subgroups of their p-localization, which is identified as a group of the same type in certain cases.
|
Open Research Newcastle | ||||||
| 2018 |
Bywaters T, Glöckner H, Tornier S, 'Contraction groups and passage to subgroups and quotients for endomorphisms of totally disconnected locally compact groups', Israel Journal of Mathematics, 227, 691-752 (2018) [C1]
|
Open Research Newcastle | ||||||
| Show 2 more journal articles | ||||||||
Software / Code (1 outputs)
| Year | Citation | Altmetrics | Link |
|---|---|---|---|
| 2021 | Tornier S, Hannouch K, 'UGALY: Universal Groups Acting LocallY' (2021) [N1] | Open Research Newcastle |
Thesis / Dissertation (2 outputs)
| Year | Citation | Altmetrics | Link | ||
|---|---|---|---|---|---|
| 2018 |
Tornier S, 'Groups Acting on Trees and Contributions to Willis Theory' (2018)
|
||||
| 2013 |
Tornier S, 'On a theorem of Shalom' (2013)
|
Grants and Funding
Summary
| Number of grants | 4 |
|---|---|
| Total funding | $470,008 |
Click on a grant title below to expand the full details for that specific grant.
20211 grants / $422,343
Effective classification of closed vertex-transitive groups acting on trees$422,343
advance our knowledge of zero-dimensional symmetry, a frontier in symmetry research. In the longer term,
advancements in fundamental knowledge in this area have the potential to inform the usage and development of
digital structures in more practical contexts, such as data networks and information processing. The project is
expected to develop new tools of both theoretical and computational nature that will accelerate ongoing research
across the field and enable new approaches. This will cement Australia's position at the forefront of research in
symmetry and its use in the digital age.
Funding body: ARC (Australian Research Council)
| Funding body | ARC (Australian Research Council) |
|---|---|
| Project Team | Dr Stephan Tornier, Dr Stephan Tornier |
| Scheme | Discovery Early Career Researcher Award (DECRA) |
| Role | Lead |
| Funding Start | 2021 |
| Funding Finish | 2023 |
| GNo | G1901376 |
| Type Of Funding | C1200 - Aust Competitive - ARC |
| Category | 1200 |
| UON | Y |
20201 grants / $2,000
SISP Program: What is Symmetry?$2,000
Funding body: Department of Education and Training, NSW
| Funding body | Department of Education and Training, NSW |
|---|---|
| Scheme | SISP Program |
| Role | Lead |
| Funding Start | 2020 |
| Funding Finish | 2020 |
| GNo | |
| Type Of Funding | C1600 - Aust Competitive - StateTerritory Govt |
| Category | 1600 |
| UON | N |
20172 grants / $45,665
Closure of projections of lattices in products of trees$45,000
Funding body: Swiss National Science Foundation (SNSF)
| Funding body | Swiss National Science Foundation (SNSF) |
|---|---|
| Project Team | Stephan Tornier |
| Scheme | Doc.Mobility |
| Role | Lead |
| Funding Start | 2017 |
| Funding Finish | 2017 |
| GNo | |
| Type Of Funding | C3212 - International Not for profit |
| Category | 3212 |
| UON | N |
Workshop: Group actions and cohomology in non-positive curvature$665
Funding body: Swiss Mathematical Society
| Funding body | Swiss Mathematical Society |
|---|---|
| Project Team | Stephan Tornier |
| Scheme | Travel Grant |
| Role | Lead |
| Funding Start | 2017 |
| Funding Finish | 2017 |
| GNo | |
| Type Of Funding | C3212 - International Not for profit |
| Category | 3212 |
| UON | N |
Research Supervision
Number of supervisions
Current Supervision
| Commenced | Level of Study | Research Title | Program | Supervisor Type |
|---|---|---|---|---|
| 2024 | PhD | Local Action Diagrams and the Scale Function | PhD (Mathematics), College of Engineering, Science and Environment, The University of Newcastle | Principal Supervisor |
Past Supervision
| Year | Level of Study | Research Title | Program | Supervisor Type |
|---|---|---|---|---|
| 2025 | PhD | Higman-Thompson Groups of Unfolding Trees of Rooted Graphs | PhD (Mathematics), College of Engineering, Science and Environment, The University of Newcastle | Co-Supervisor |
| 2024 | Masters | On the Unitary Representation Theory of Contraction Groups | M Philosophy (Mathematics), College of Engineering, Science and Environment, The University of Newcastle | Co-Supervisor |
| 2024 | PhD | Elementary Topological Groups | PhD (Mathematics), College of Engineering, Science and Environment, The University of Newcastle | Co-Supervisor |
News
News • 13 Apr 2022
First mathematical software recognised as Non-Traditional Research Output
Researchers from the School of Information and Physical Sciences impressed the University’s Non-Traditional Research Output (NTRO) Committee recently with an innovative software package for analysing mathematical structures. This is the University’s first software output and has been confirmed by the Committee as being recognised internationally.
News • 23 Nov 2020
Four Newcastle researchers selected for funding boost
University of Newcastle researchers have received more than $1.6m in grants from the Australian Research Council’s Discovery Early Career Researcher Award (DECRA) scheme.
News • 4 Jun 2019
Special Semester at the Bernoulli Center
The research group around ARC Laureate Fellow George Willis was recently granted a special semester at the Bernoulli Center in Lausanne, Switzerland to take place in the second half of 2020.
Dr Stephan Tornier
Position
ARC DECRA
School of Information and Physical Sciences
College of Engineering, Science and Environment
Contact Details
| stephan.tornier@newcastle.edu.au | |
| Phone | 0240550960 |