Adaptive Discontinuity Layout Optimization

Key Researchers: Mason Crumpton, Andrew Abbo

Discontinuity Layout Optimization (DLO) is an innovative geotechnical stability analysis method which computes rigorous upper-bounds on the loads that cause collapse in a body of soil. The method is well suited to the development of general-purpose software and is simple to apply in practice, making it an attractive option to competing techniques. However, the method demands that large optimisation problems be solved which is only feasible if smart algorithms are used. Research within the Centre has led to the development of an Adaptive Discontinuity Layout Optimisation (ADLO) algorithm which improves the computational performance of DLO through the use of mesh refinement and enhancements to the core solution procedure.

In principal, DLO works by identifying an optimum collapse mechanism within a mesh of slip lines or velocity discontinuities that are constructed by making connections between pairs of nodes in a grid. Allowing discontinuities to intersect means that the number of connections in a mesh increases rapidly with the number of nodes. This permits an enormous range of potential collapse mechanism geometries but results in large linear optimisation problems. These are solved in an iterative fashion by first considering the system of equations for a small subset of the discontinuities in a mesh and then gradually adding equations for the remaining discontinuities until an optimum mechanism is obtained.

The ADLO algorithm developed by Centre investigators, reduces the computational effort required for an analysis by adaptively refining meshes so that fewer nodes are needed to obtained a given solution accuracy, and enhancing the iterative DLO solution procedure to improve the speed at which it converges. The adaptive scheme works by using the results of an initial analysis to identify critical regions where mesh refinement is likely to improve accuracy, it then adds new nodes to these regions before re-analysing the problem. This process of refining and re-analysing is continued until the desired degree of solution accuracy is obtained.

To implement the ADLO algorithm new techniques for estimating the interpolation errors throughout a mesh and rapidly constructing large sets of non-overlapping discontinuities on arbitrary clouds of nodes have been developed. The later of these techniques is based on the novel concept of geometric duality.

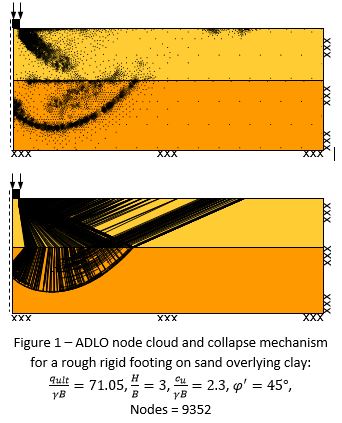
Figure 1. shows the refined node cloud and corresponding collapse mechanism produced by ADLO for the analysis of a rough rigid strip footing bearing on sand overlying clay. For this example, it was found that the ADLO algorithm required less than 1 minute to deliver a solution with an accuracy in the order of 1% while an equivalent non-adaptive analysis required approximately 1hr. The variables governing the stability of this problem were the ultimate load (q_ult), footing width (B), sand depth (H), sand friction angle (𝜑′), sand unit weight(y), and clay undrained shear strength(c_u).