
Remote sensing near-Earth space
Human communications and surveillance technology is firmly in place in space. There are many objects floating about in space including nuts and bolts, discarded gloves and fragments from exploded spacecraft. Since the launch of Sputnik in 1957 (to Jan 2008) there have been 4600 launches that have placed 6000 satellites into space, with ~400 of these travelling beyond Earth orbit. Of the remaining 5600, only ~800 are still working.
Space covers a large volume and the sensor instrumentation are few, so a ground based, remote sensing method has been developed to monitor the base-load plasma mass density for Space Physics research. This was developed at Newcastle using naturally occurring ultra-low frequency (ULF; 1-100 mHz) field line resonances. The shear Alfven magnetised plasma wave mode in space has its energy guided along the magnetic field. When the wave energy encounters the ionosphere, part of the energy reflects back into space. At the appropriate frequency, a field line resonance (FLR) is formed.
The basic idea for remote sensing is to detect the resonance signature of these resonant low frequency plasma waves. The best way is to use the cross phase of magnetometer data recorded at ~100 km spaced (north-south) locations. This information may then be used to estimate the plasma mass density in space.
The procedure to remote sense the plasma mass density in the magnetosphere as a function of both time and radial distance is as follows.
- Obtain the ULF magnetometer data from two latitudinally spaced (~100 km) sensors
- Calculate the ULF resonant frequencies. For an example, see Waters et al., (1991)
- Solve the ULF wave equation for the plasma mass densities
This process yields an estimate of the plasma mass density in the equatorial plane, tracking out into space along the magnetic field from the location of the magnetometers on the Earth surface.
Solving the wave equation requires that the magnetic field topology be known. At low latitudes we use the International Geomagnetic Reference Field (IGRF) and for high latitudes we use the IGRF with the Tsyganenko models. The integration of the Tsyganenko magnetic field models was done in collaboration with Dr Eric Donovan, now at University of Calgary, Canada. This work was reported in J. Geophys. Res., 101, p24737, 1996.
 Figure 1 |
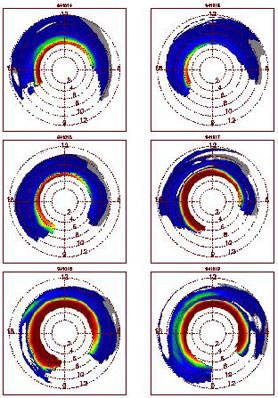 Figure 2 |
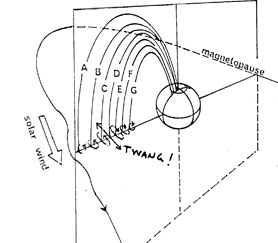 Figure 3 |
The University of Newcastle acknowledges the traditional custodians of the lands within our footprint areas: Awabakal, Darkinjung, Biripai, Worimi, Wonnarua, and Eora Nations. We also pay respect to the wisdom of our Elders past and present.
